Internal Waves 4 - Impulse
Purpose:
To show the unusual, anisotropic phase and group velocity properties
of internal waves in a density-stratified fluid.
What Happens:
A tank about 30 cm deep is filled with a salt stratification of
buoyancy period, 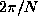 ,
about 6 seconds. A solid cylinder of a
few cm diameter runs across the tank at mid depth, in the right of the
field of view. This cylinder is oscillated horizontally (to the left
and right) at frequency less than N, generating internal waves. The
flow is visualized with a schlieren system that shows regions of
positive isopycnal slope in red. Slopes close to zero show as yellow.
The movie is in time lapse, so that the waves appear to have higher
than real frequency. The movie starts from rest, and after the paddle
motion begins, the wave field starts to fill the tank outwards from
the paddle. The paddle motion is a brief impulse, so the energy
contains all frequency components.
,
about 6 seconds. A solid cylinder of a
few cm diameter runs across the tank at mid depth, in the right of the
field of view. This cylinder is oscillated horizontally (to the left
and right) at frequency less than N, generating internal waves. The
flow is visualized with a schlieren system that shows regions of
positive isopycnal slope in red. Slopes close to zero show as yellow.
The movie is in time lapse, so that the waves appear to have higher
than real frequency. The movie starts from rest, and after the paddle
motion begins, the wave field starts to fill the tank outwards from
the paddle. The paddle motion is a brief impulse, so the energy
contains all frequency components.
Physics of the phenomenon:
a. Dispersion relationship
(See "Internal waves 1 - low freqency".)
If one considers
disturbances of the form 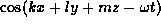 ,
then those disturbances
must obey the dispersion relation for internal gravity waves
(Phillips, 1966):
,
then those disturbances
must obey the dispersion relation for internal gravity waves
(Phillips, 1966):
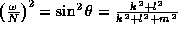
This means that the frequency depends on the angle
 , which is the
angle the wave crests and the wave energy flux or group velocity make
to the horizontal. Waves of a specific frequency can only propagate
at a specific angle, different for each frequency.
, which is the
angle the wave crests and the wave energy flux or group velocity make
to the horizontal. Waves of a specific frequency can only propagate
at a specific angle, different for each frequency.
b. Group velocity:
The energy is carried outwards from the paddle by the group velocity,
which is restricted to the characteristic angles 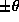 , which are
different for each frequency component. Therefore each frequency
component travels at a different angle away from the paddle.
, which are
different for each frequency component. Therefore each frequency
component travels at a different angle away from the paddle.
c. Phase velocity
The wave "crests", or lines of constant phase, are the red bands.
Note that they sweep perpendicular to the energy rays: the phase
velocity is perpendicular to the group velocity. The resulting
pattern looks like a pattern of radial bands that constantly sweep
towards the horizontal.
d. Effects of reflection
After the wave field develops, the red bands start to appear "lumpy".
This is because the waves that travel to the right from the paddle are
reflected from the right-hand tank wall, and the reflected waves start
to interfere with the original ones. This can be thought of
mathematically as the interference pattern produced by the waves from
an "image" wavemaker located to the right of the tank wall.
References:
Phillips, O.M. 1966. The dynamics of the upper ocean. Cambridge
University Press.
Lighthill, James, 1978. (Chapters 3 and 4) Waves in fluids. Cambridge
University Press.
Credits:
Movie and text - Barry Ruddick
Digitization of movie - Dave Hebert
Load and run impulse internal waves movie
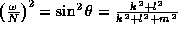
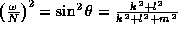
![]() , which is the
angle the wave crests and the wave energy flux or group velocity make
to the horizontal. Waves of a specific frequency can only propagate
at a specific angle, different for each frequency.
, which is the
angle the wave crests and the wave energy flux or group velocity make
to the horizontal. Waves of a specific frequency can only propagate
at a specific angle, different for each frequency.